Inverse Gas Chromatography at Finite Concentration (IGC-FC)
Principle of IGC-FC
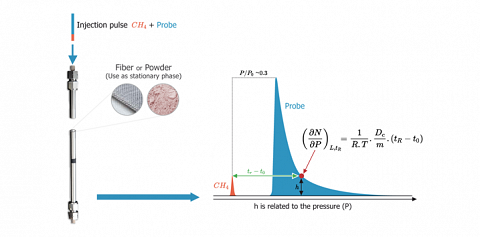
Inverse Gas Chromatography at finite concentration conditions (IGC-FC) is a dynamical method providing readily adsorption isotherms. The usual procedure, called ECP (Elution at the Characteristic Point), allows to determine from a single chromatographic peak part, the isotherm of desorption for relative pressures $(P⁄P_0)$ ranging from near zero to 0.3 and above.
This kind of chromatography is performed by injecting, usually in the liquid form, known amounts of solutes (molecular probes) in the GC column containing the solid of interest. Depending on the nature of the solids, those quantities are between a tenth and some twenty microliters ($\mu L$). After the injection, the solutes are vaporized. Carried by the “carrier gas”, the solutes occupy successively the whole surface of the solid before being ejected. The solute flow is then detected and recorded.
The analysis of the chromatogram, as depicted here above, leads to desorption isotherms and adsorption energy distribution of the sites explored by the solute molecules.
Determination and exploitation of the desorption isotherms
The analysis of the diffuse front of the chromatogram readily provides the desorption isotherm of the injected probe molecule.
The first derivative of the isotherm is directly related to the neat retention time characterized by each point of the chromatogram.$$\left( \frac {\partial N}{\partial P} \right)_{L,t_R} = \frac {1}{R.T}.\frac {D_c}{m}.(t_R-t_0)$$
$L$ is the length of the column, $N$ is the number of molecules at each point, $P$ is the adsorption pressure, $t_R$ is their retention time and $t_0$ (the retention of a poorly adsorbing solute such as methane) allows to calculate the dead volume. $D_c$ is the corrected gas flow and m the mass of solid inside the column.
Furthermore, the solute pressure is directly related to the height of the signal at the given point. The chromatogram delivers all necessary information for the determination of the desorption isotherms.
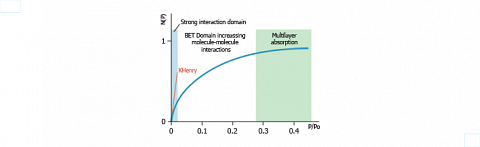
The computed isotherms are split into several domains, as depicted on the above example. The first domain, located at low relative pressure, corresponds essentially to strong solute-solid surface interactions. This represents the linear part of the isotherm whose slope provides the Henry constant (KHenry).
The part of isotherm corresponding to relative pressures between 0.05 and 0.3 allows the evaluation of the specific surface area and BET constant by application of the BRUNAUER, EMMETT and TELLER (BET) theory. That part of the isotherm describes weak solute-solid interactions whereas solute-solute interactions become prevalent.
The final part of the isotherm, where multilayer formation occurs, is usually not considered in chromatography.
Determination of the surface energetic heterogeneity
All solid surfaces are heterogeneous. This heterogeneity has various origins: geometrical, energetic or chemical. IGC-FC delivers a “fingerprint” of the surface heterogeneity in the form of adsorption energy distribution of the various sites.
Moreover, this method, using probe molecules of different morphology and functionality, allows acceding to the different aspects of the surface heterogeneity.
Yet the actual determination of those distribution functions is far from being evident. The paper by Charmas and Leboda lists the difficulties and suggests the solutions proposed by the various authors.
The mathematical problem stems from the resolution of the first order Fredholm integral function that gives access to the energy distribution $\chi (E)$). No simple way exists to solve that problem:$$N(P_m,T_m)=N_0. \int_{E_{min}}^{E_{max}}\theta (E_min)(E,P_m,T_m).\chi(E).dE$$
$N(P_m,T_m)$ is the number of adsorbed molecules at pressure $P_m$ and at temperature $T_m. N_0$ represents the number of molecules required to form a monolayer. $\theta (E,P_m,T_m)$ is the local isotherm and $E$ the adsorption energy on a given site.
The physicochemical problems are related to the validity and meaning of the simplifying hypotheses that allow the resolution of the integral. They also stem from the ignorance of the solute-solute interactions that significantly intervene at the higher degrees of solid surface coverage’s.
To overcome those problems, one may apply the method developed by Balard (1997). For the sake of simplicity, the mathematical approach will not be given here. Only the hypotheses behind this approach will be discussed.
The first step is the correction of the multilayer part of the adsorption isotherm to restrict the interpretation to the sole probe-surface interactions. Thereafter, the computing of the distribution function with the condensation approximation (CA) is performed (FDCA). The model of the surface is the patchwork as shown here after, where each domain is supposed to be homogeneous.
Each domain is described by a “local” isotherm”. The sum of the local isotherms reconstructs the observed (but multilayer corrected) isotherm. The condensation approximation greatly simplifies the FREDHOLM equation by reducing the local isotherm $\theta(E,P_m,T_m)$ to a constant value (0, 1/2, or 1), depending on the adsorption energy and characteristic pressure of the sites.
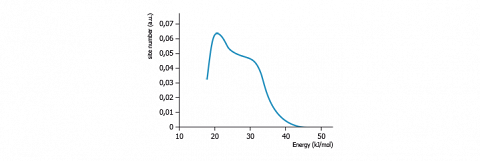
The FDCA are generally rather coarse as depicted here above. The resolution of those functions is improved when eliminating the computation background noise, and applying the RUDZINSKI-JAGIELLO method. The method of BALARD smoothes the FDCA using FOURIER series that easily gives access to multiple derivatives required in the RUDZINSKI-JAGIELLO method.
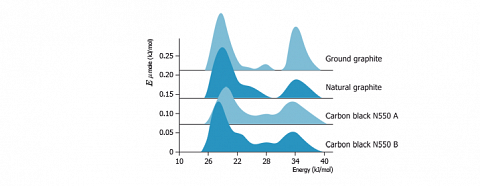
Those energy distribution functions allow to observe the various components that constitute the FDCA. As an example, the figure hereafter presents the results obtained with heptane (at 40 °C) on various carbon materials.
Molecular probes (adsorbates)
The characteristics of the molecules able to be used as probes are the following:
- vaporisable,
- must be detected by the instrument,
- thermally stable during the experiment,
- only able of reversible adsorption,
- eluted in a reasonable time.
The classical used probes are:
- n-alkanes (pentane→dodecane),
- branched and cyclic alkanes (pentane→octane),
- Polar molecules
- alcools, acids, ethers, ketones, esters…
- amines…
- aromatics…
The advantage of this method is to be able to perform measurements at temperatures close to the application and with molecules representative of the application.