Surface morphology
Ligner et al. (1989-1990) measured the value of the dispersive component of the surface energy ($\gamma^d_s$) of H-Magadiite at around 285 mJ/m2. Such a value is especially high. They also observed that the octane branched isomers were eluted about 10 times faster than their linear isomer n-octane. Obviously, such a difference cannot be justified by the difference in polarizability induced by the alkane branched structure.
The structure of H-Magadiite being lamellar and able to intercalate organic molecules, the authors attributed this particular behaviour to the inclusion of n-alkanes in some sites, which were inaccessible to branched probes due to a size exclusion phenomenon.
The appreciation of the importance of the size exclusion phenomenon requires an adapted molecular descriptor that takes into account the influence of the structure on the polarizability.
Brendlé and Papirer (1997a) proposed the $\chi_T$, a molecular descriptor based on the Wiener index ($W$). Wiener introduced his index in 1947 that is the oldest topological index related to molecular branching. It was shown that the Wiener index number is closely correlated to numerous physicochemical properties of the molecules (e.g. the boiling points of alkane molecules). Other works on quantitative structure–activity relationships showed that it is also correlated with other parameters like density, surface tension, viscosity and the Van der Waals surface area and volume of the molecule.
Therefore, $W$ and $\chi_T$ can also be employed to describe the polarizability of the molecules i.e. to their capacity to exchange dispersive interactions. Moreover, a linear relationship between the polarizability and $\chi_T$ was found (Balard et al. 2000a). The main advantage of the latter is that they can be calculated for probes, for which no data is present in the literature.
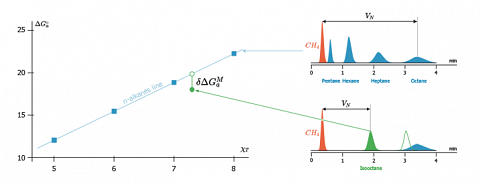
The figure hereafter displays the chromatograms acquired for some linear alkanes probes and for isooctane, on a solid exhibiting a strong size exclusion effect for branched isomers. This figure also displays the diagram (left) obtained when plotting the free energy of adsorption of the probes versus their descriptor ($\chi_T$).
On this chromatogram, the hollow signal shows the position that the isooctane peak would have if no exclusion phenomenon would exist, i.e. if the surface is planar at the molecular level.On the left diagram, the corresponding representative point (the hollow circle) is then situated on the alkanes line. This is what is observed, for example, in the case of some pyrogenic silicas having a mean surface area value. The flatness of such pyrogenic silicas (SBET=130 m2/g) was confirmed by other methods.
In contrast, if the surface is nanorough some size exclusion effect exists and the isooctane probe takes place bellow the n-alkane straight line (black circle). The exclusion of isooctane from sites, in which n-alkanes could be inserted, will induce a decrement of free energy $\delta \Delta G^M_a$. This decrement is equal to the ratio of the measured retention volume of the branched probe ($V_N$) on that it would have if it was not excluded ($V^{ref}_N)$. The morphology index $IM$ is then defined according to the equation:$$IM=\exp \left[\delta \Delta G^M_a \right]=\frac{V_N}{V^{ref}_N}$$
Thus a value equal to 1, or very close, indicates that the surface accessibility of branched molecules is identical to that of linear alkanes. Thus, the surface could be considered as flat at the molecular level. If the morphology index is less than 1, then a surface nanoroughness takes place. Lower the morphology index is, the higher the surface roughness at the molecular level is.
Some example of measured $IM$ values are given on the table hereafter.
|
Examples of $IM$ values
|
|||||
| Solides | S (m2/g) | $IM(\chi_T)$ | |||
| Cyclohexane | DiMethylHexane | TriMethylPentane | TetraMethylButane | ||
| Silice | 130 | 0.95 | 0.91 | 1.1 | 1.1 |
| Talc | 4 | 0.52 | 0.32 | 0.41 | |
| H-magadiite | 80 | 0.19 | 0.13 | 0.09 | 0.11 |
We observe that these size exclusion effects are very common, the flatness the exception. Pyrogenic silicas of high specific surface area exhibit a high surface roughness associated to the imperfect coalescence of protoparticles at the nanoscale (Balard et al. 2000b). For lamellar solids, like clays and talcs, the surface roughness is due to the presence of like slot sites present on the side surfaces of the crystals (Comard et al. 2001a). In the case of carbon black, the phenomenon of exclusion is related to the particular structure like fish scales made of graphite planes, proven by STM (Calvet et al 2012), then the n-alkane probes could be inserted at the edge of the scales.
It is also important to note that the nanoroughness of the surface explains the measured high $\gamma^d_s$ values. Indeed, nanoroughness implies that the adsorbed n-alkane probes are probably in contact with more than one surface. In other words, the dispersive interactions between the surface and the probes become even stronger.
The molecular descriptor $\chi_T$ used to estimate the surface roughness, could be also used to describe molecules comprising heteroatoms, i.e. polar molecules. Therefore $\chi_T$ is also useful for the measurement of the strength of the specific interactions with the surface.