Polar character and acid base properties
The specific or polar interactions involve all type of interactions except the dispersive interaction or London interaction by instantaneous dipoles. They can be polar, ionic, magnetic, electric or acid-base. These acid-base interactions are largely predominant according to Mittal and Anderson (1991).
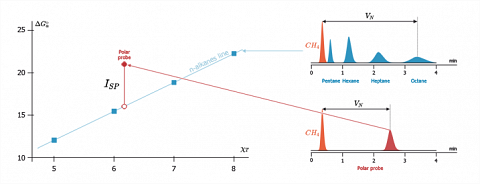
Just as for the morphology indexes, the specific interaction parameters ($I_{SP}$) will be determined with reference to the n-alkane straight line. This is achieved by considering that the gap of free energy change of adsorption between the representative point of the polar probe ($\Delta G_a$) and its projection on the alkanes straight line ($\Delta G^{d}_a$), will correspond to the contribution of the specific interactions ($\Delta G^{SP}_a$). So the $I_{SP}$ of a probe is given, in kJ/mole, by the following expression:$$I_{SP}=\Delta G^{SP}_a=\Delta G_a-\Delta G^d_a$$
The figure hereafter illustrates the $I_{SP}$ determination method, which allows the easy splitting of the free adsorption enthalpy, into a dispersive term ($\Delta G^d_a$) and a specific term ($I_{SP}$).
Here, the molecular descriptor ($\chi _T$) is calculated like for the alkanes, by taking into account the geometry of the polar probes [Brendlé and Papirer (1997b)]. As for the alkane probes, the $\chi _T$ parameters of the polar probes correlate well with the literature data concerning their polarizabilities [Balard et al. (2000a)].
Historically, other molecular descriptors have been proposed. So Saint Flour and Papier (1983) retained as parameter the logarithm of the vapour pressure of the probe ($\log ({P_0})$).
Then Schultz and al. (1987) proposed the product of the molecular area of the probe ($\log (P_0)$) by the square root of the dispersive component of its superficial pressure ($\gamma^d_s$) that is ($a.\sqrt {\gamma^d_s}$).
The first parameter suffers to be related to the cohesion energy of the liquid, hence to the interaction energy between two identical molecules. The second parameter overcomes partially this fault, in referring to the dispersive component of the liquid. But it supposes also the knowledge of the adsorption area, which cannot exactly be known, because it varies with the conformation of the molecule in the adsorbed state. Despite that, it is still used.
These limitations justify the choice of a descriptor ($\chi _T$), which is directly related to the polarisability of the probe and easily accessible by computation.
By diversifying the functionality and the acid-base character of the injected molecule, it becomes possible to have access on the acid-base character of the studied solid.
Determination of the acidity and basicity constants of the solid. ($K_A$, $K_B$)
The acidity and the basicity constants of a solid can be determined by injecting polar probes whose electron acceptor ($AN$) and donor number ($DN$) are known.
These numbers belong to the semi-empirical scale of Gutmann (1978), corrected by Mukhopadhyay P., Schreiber (1995). The $I_{SP}$ of a probe is related to its constants $DN$ and $AN$ and to the acid $K_A$ and Basic $K_B$, of the solid by equation:$$I_{SP}=DN.K_A+AN.K_B$$
Where $DN$ and $AN$ are respectively the electron donor and acceptor numbers and KA and KB, those of the solid surface.
In fact, this relation describes the interaction between two amphoteric partners. The values of constants KA and KB are finally determined by transforming the previous equation as following:$$\frac{I_{SP}}{AN}=\frac{DN}{AN}.K_A+K_B$$
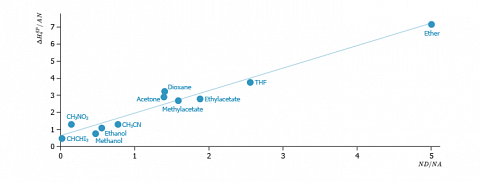
An example of application of this method to the determination of the acid-base character of a cellulose is depicted on the figure below.
We can notice that a satisfactory linear relation is obtained. The slope gives the acid surface constant ($K_A$) whereas the ordinate gives the basic surface constant ($K_B$).
The $K_a$ and $K_B$ values are suitable to compare the acid-base character of different solids as displayed on the last figure.
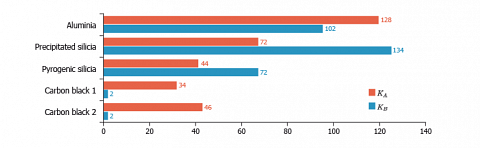
We can see that the carbon blacks are mainly, but weakly basic. The pyrogenic silica presents a major acid character attributed to the presence of surface silanol groups. The precipitated silica, which is more hydroxylated, exhibits higher acid-base constants. Finally the aluminium oxide that carries important basic and acid sites, has clearly a more pronounced amphoteric character.