Inverse Gas Chromatography at Infinite Dilution
The inverse gas chromatography at infinite dilution (IGC-ID) consists in injecting very small amounts of probe molecules into a chromatographic column containing the solid to be investigated. The degree of dilution is such that intermolecular interactions between the adsorbed molecules can be neglected.
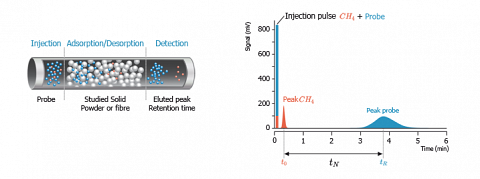
Practically, a pulse of very diluted vapour of probe molecules is injected into the column. Pushed by the carrier gas, the probe molecules explore statistically the whole surface of the solid before leaving the column. The flow of solute molecules leaving the column is then detected and recorded. A chromatogram is then obtained then as displayed on the figure hereafter.
When progressing inside the CG column, the probe molecules undergo numerous adsorption-desorption cycles. Hence, they stay adsorbed on the stationary phase for a short or longer time, depending on the intensity of the interactions exchanged between the probe and the solid surface.
The average time spent by the solute probes in the adsorbed state is known as the neat retention time ($t_N$). The value of $t_N$ is equal to the difference between the retention time of the peak of the probe and the retention time of a non-retained probe like the methane ($t_0$), which doesn’t adsorb at the measurement temperature.$$t_N=t_R-t_0$$
Generally the taken value for $t_R$ corresponds to the first order moment of the peak of the probe.
From neat retention time value $t_N$, we deduce the volume of the carrier gas required to push the solute out of the chromatographic column. This volume is known as the net retention volume ($V_N$) and is computed by multiplying the net retention time by the flow rate ($D$):$$V_N=D.J.t_N$$
Where $J$ is the James Martin coefficient that takes into account the expansion of the gas inside the column bound to the pressure gradient. $J$ is given by the following equation where $P_E$ is the entering pressure and $P_A$ the atmospheric pressure.$$J=\frac{3}{2}.\left(\frac{(P_E/P_A)^2-1}{(P_E/P_A)^2-3}\right)$$
Starting from the $V_N$ value of one or several probes it is possible to determine:
- The solubility parameters of a deposited polymer (melted) on a chromatographic support, by injection of a series of chosen probes.
- The diffusion coefficient of probes into a thin polymer film supported by a solid.
- The standard free energy change of adsorption $\Delta G^{\circ}_a$ of the probe on a solid surface.
The chromatographic process results from the equilibrium between the mobile phase and the stationary phase. For a solid, $V_N$ is connected with the equilibrium constant ($K$) and the total adsorption area ($A$) of the solid contained in the column as follows:$$V_N=K.A$$
Specifically at infinite dilution conditions, $V_N$ is directly related to the standard free energy change of adsorption $\Delta G^{\circ}_a$ of the probe on the surface, by:$$\Delta G^{\circ}_a(probe)=-R.T.\ln (K)=-R.T.\ln (V_N)+C$$
Where $C$ is a constant depending on the choice of a bi-dimensional reference state.
For melted polymers, the tri-dimensional reference state is usually used. But for the adsorption on a solid, quite arbitrary bi-dimensional reference states have been proposed. Most of them are assuming the surface homogeneity. But the real solid surfaces are in general more complex and heterogeneous. Therefore, the application of these bi-dimensional reference states was considered as inappropriate.
The most often, the authors overcome the choice by computing the free energy change of adsorption as follows:$$\Delta G_a(probe)=-R.T.\ln (V_N)$$
It is also possible to determine parameters that are independent of the reference state:
- The adsorption enthalpies obtained from the variation of the free energy with the temperature. The study of their variation with the temperature allows the detection of transition temperature of the first order or the second order.
- The free energy increments of homologous series of linear alkane or oligomers allow acquiring data related to the surface energy.
Doris and Gray have taken this approach to develop a determination method of $\gamma^d_s$, the dispersive component of the surface energy.