Dispersive component of the surface energy ($\gamma^d_s$)
This determination is performed with IGC-ID, i.e. Inverse Gas Chromatography at Infinite Dilution, and was first proposed by Dorris and Gray (1979).
For that purpose, they measured the retention time ($t_N$) of a series of n-alkane molecular probes. With respect to the infinite dilution conditions, the measured retention times are directly related to their free energy change of adsorption ($\Delta G_a$) as follows:$$\Delta G^{\circ}_a(probe)=-R.T.\ln (V_N)+C$$
With $T$ the measurement temperature and $V_N$ the net retention volume and $C$ a constant depending on a theoretical bi-dimensional reference state for the adsorbed molecules.
In order to avoid the use of this reference state (several exist), they proposed an approach based on the fact that, for n-alkanes, $\Delta G^\circ_a$ the free energy change of adsorption varies in a linear way with the number of their carbon atoms. Such a linear behaviour is shown on the figure here after.
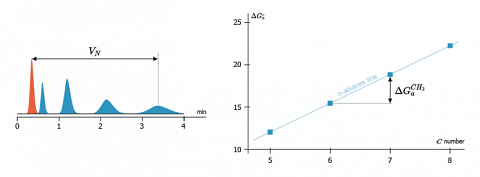
With help of this linear behaviour, a free energy increment by methylene group ($\Delta G^{CH_2}_a$) is determined. It corresponds to the slope of the n-alkanes line and is no more depending from $C$. $$\Delta G^{CH_2}_a=R.T.\ln \left( \frac{V_{N}+1}{V_{N}}\right)$$
The n-alkane probes are non-polar and only able to exchange non-specific interactions with the surface (London Forces). Therefore, the work of adhesion of the methylene unit to a surface $W^{CH_2}_a$, as described by Fowkes (1967), can be written: $$W^{CH_2}_a=2N.a_{CH_2}.\sqrt{\gamma^d_s.\gamma_{CH_2}}$$
With $a_{CH_2}$ the area of a methylene unit, $N$ the Avogadro’s number and $\gamma_{CH_2}$ the superficial energy of a solid made only of methylene units (i.e. polyethylene).
Since the adsorption and the work of adhesion are reversible, we can bring them closer:$$\Delta G^{CH_2}_a=W^{CH_2}_a$$
By combining the two last equations, we can calculate the dispersive component of the surface energy $\gamma^d_s$:$$\gamma^d_s=\frac{1}{\gamma_{CH_2}}.\left[ \frac {\Delta G^{CH_2}_a}{2N.a^{CH_2}_a}\right]^2$$
It is worth to underline that this approach supposes that the n-alkane probes adsorb flat on the surface and that the surface is homogeneous.
The table below reports some range of values of the $\gamma^d_s$ values measured on different types of solids.
| Solids | $\gamma^d_s(mJ/m^2)$ |
| Polymer | 25 to 60 |
| Cellulosis | >35 to 55 |
| Calcium carbonate | 33 to 110 |
| Talcs | 110 to 200 |
| Carbon blacks | 80 to 550 |
We can see that for a given type of solid, the dispersive component can vary in a large range.
The dispersive interactions are strongly related to the polarizability of the surface. In the case of carbon blacks, a large variability of the measured $\gamma^d_s$ values is observed. Especially, the highest values are measured on conducting carbon blacks. This can be explained taking into account the fact that, for these solids, the electrons are much mobile, i.e. more polarisable.
But this explanation does not match for the calcium carbonates, neither for talc. Indeed, both solids are insulators and also show high variability of their $\gamma^d_s$ values.
One question arises: Are assumptions made for the computation of the $\gamma^d_s$ value respected?
More precisely: is the surface of the examined solid smooth and homogeneous? We will see that the IGC-ID is also able to give access to information about the surface morphology at the molecular probe scale.
