Transition and crystallinity
Since 1969, Guillet and his co-workers have initiated the use of IGC for the measurement of the glassy transition temperature of a polymer deposited on a solid support [Lavoie and Guillet (1969)]. Other works have been done on the influence of the tacticity of a PMMA deposited on an alumina on the $T_g$ by Braun and Guillet (1975), Hamieh and al (1988). Hamdi and al (2002) have also studied the influence of the impregnation ratio on the $T_g$ of a PMMA deposited on pyrogenic silica. Finally, a review on the subject was done by Nastasovic and Onjia (2008).
The method generally applied for the study of the polymer transition consists in representing the variation of the retention volume $V_g$ versus the reciprocal of the absolute temperature of the column. Such a representation is called retention diagram or Van't Hoff retention diagram. This variation is generally linear and the slope is related to the enthalpy of the process, solution in the liquid stationary phase or adsorption on the solid surface, if solid material is in the column. The relationship is shown by the equation hereafter. Thus:$$\frac{\partial \ln (V_g)}{\partial(1/T)}=-\frac{\Delta H}{R}$$
Here $-\Delta H$ is the corresponding enthalpy, $R$ is the gas constant and $V_g$ the specific retention volume. $V_N$ is directly related to the neat retention volume as follow:$$V_g=\frac {1}{m}.\frac {273.15}{T}.V_N$$
Where $m$ is the mass of the solid contained in the column and $T$ the measurement temperature in Kelvin.
The Van't Hoff retention diagram displays a linear relationship so long the sorption process (adsorption or absorption) is invariant. It is not the case if a transition phenomenon occurs. We will then observe singularities as shown on the figure here after.
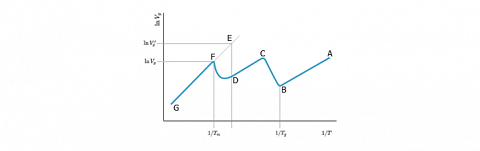
The AB segment corresponds to a temperature domain, in which the polymer is under its glass transition temperature ($T_g$). In this temperature domain, only the adsorption at the polymer surface influences the retention process.
The point B corresponds to the glass transition temperature. Then, the penetration of the probe into the polymer mass starts and non-equilibrium conditions prevail to the point C where the probe can access all of the amorphous domains.
The variation of $\ln (V_g)$ in function of the reciprocal temperature becomes again linear until the fusion point $T_m$ is approached. The fusion of the crystalline domains leads to an increase of the retention volumes. At the point F, the fusion temperature Tm is reached. Thereafter, the segment FG, corresponds to the sorption process into the melting polymer layer, and a new linear relationship is observed.
The crystallinity ratio of the polymer phase could also be determined thanks to this diagram. For that purpose, the segment GF is extrapolated to the point E having the same abscissa than the point D, which matches at the beginning of the fusion of the crystalline domains. In fact, the ordinate of E would be equal to the measured value if the polymer would be completely amorphous. A crystallinity ratio can then be calculated according to the equation:$$W_\%=100. \left[ 1- \frac{V^E_g}{V^F_g}\right]$$
Where $V^E_g$ and $V^F_g$ are the net retention volumes corresponding respectively to the points E and F.
For the study of the transition temperature IGC analysis is complementary, e.g., to the DSC. In the case of polymers deposited in very thin layers on a solid, IGC is more interesting. Indeed, for very low polymer amounts, DSC is no more enough sensitive.
The next example highlights the influence of the impregnation ratio of pyrogenic silica by PMMA, on the glass transition and β transition temperatures, detected by IGC.
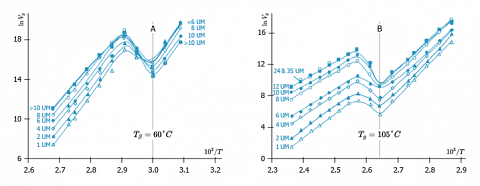
A: Detection of the $β$ transition of the PMMA at 60°C.
B: Detection of the glass transition of the PMMA at 105°C.
We observe that the positions of these two transitions are independent of the impregnation rate. However, the intensity of the observed jump increases with it. This suggests that the adsorption on a surface does not disturb the most monomers units.
The great sensitivity of this method is underlined by the fact that the transitions are still detected for a coverage ratio of only 1 UM/m2. This is corresponding to an impregnation rate of only 2,2% in mass. Therefore, IGC is a well-adapted method for the study of the thermal properties of coating or sizing.
Finally, we can underline that the evolution of the superficial properties of a solid impregnated under a controlled way by a polymer can be an approach allowing to obtain information concerning the intensity of the interaction occurring between the solid surface and the macromolecule.
